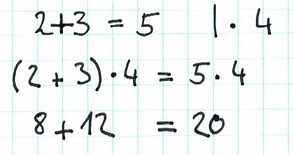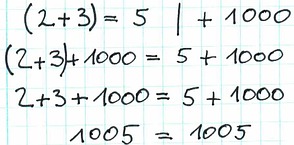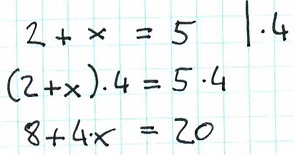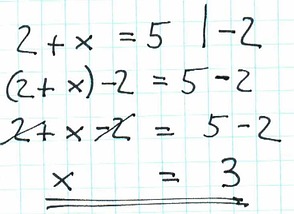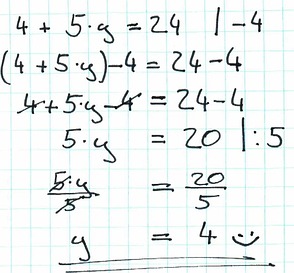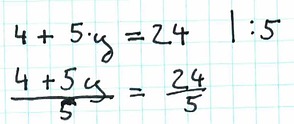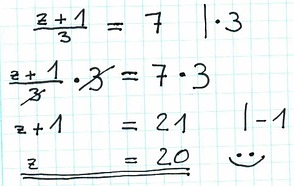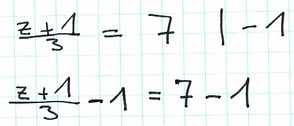Gleichungen mit einer unbekannten Variable lösen

ist nicht schwer. Hier lernt ihr wie es geht die unbekannte Variable in Gleichungen zu finden.

Dieser Artikel zeigt euch wie ihr drei verschiedene mit Gleichungen steigenden Schwierigkeitsgrad mit einer unbekannten Variable lösen lernt. Allerdings ist das sture lösen einer Gleichung nur die halbe Miete. In der Mathematik ist es besonders wichtig die Dinge nicht nur mechanisch - wie ein Roboter - rechnen zu können, sondern auch zu verstehen und den Sinn dahinter zu finden. Hier zeige ich euch nicht nur das blanke Rechnen sondern auch wie ihr die Gleichung als Ganzes verstehen könnt.

Grundlegendes zu Gleichungen

Um Gleichungen zu lösen, sollte man zuerst verstehen, was Gleichungen sind. Es steckt schon im Wort Gleichung drinnen, nämlich dass etwas gleich ist und zwar ist die linke Seite vom "Istgleichzeichen (=)"gleich der rechten Seite, z.B: 2+3=5
Nun kann man fast alles machen, solange man es für beide ganzen Seiten macht und man bekommt wieder eine gültige Gleichung. Also kann man z.B. beide Seiten mit 4 multiplizieren: (2+3)*4=5*4
Oder zu beiden Seiten 1000 addieren: 2+3+1000=5+1000

Durchstarten Mathematik 3. Schuljahr. Dein Übun...

Durchstarten Mathematik 7. Testbuch: 3. Klasse ...

Gleichung mit einer unbekannten Variable => 2+x=5

Soweit so gut, nun zu einer Gleichung mit einer Variablen: 2+x=5

Eine Variable (in dem Fall x) ist ein Platzhalter für eine noch unbekannte Zahl. Wir wissen aber bereits, dass wir alles machen dürfen, solange es wir für beide Seiten machen. Wir dürften nun alles machen (z.B. beide Seiten mit 4 multiplizieren): (2+x)*4=5*4

Das dürften wir machen, bringt uns aber in diesem Fall nichts und trägt nichts zur Auflösung dieser Gleichung bei. Wir wollen ja herausfinden, was x ist. Was uns dabei weiterhilft, ist bei beiden Seiten 2 zu subtrahieren: (2+x)-2=5-2

Das ist schon alles, was wir gleichungsumformungsmäßig machen müssen, um x herauszubekommen. Nun müssen nur mehr beide Seiten ausrechnen.

Als erstes die Klammer auflösen, was in diesem Fall einfach weglassen der Klammer bedeutet: 2+x-2=5-2

Man kann klar sehen, dass auf der linken Seite 2 und -2 sich gegenseitig aufheben und nur x übrigbleibt. Auf der rechten Seite ergibt 5-2 gleich 3.

Also bleibt unterm Strich: x=3 und die Gleichung ist gelöst.

Die zweite Gleichung ist ein wenig schwieriger => 4+5*y=24

Nun kommen wir zu einer anderen, ein bisschen schwierigeren Gleichung. 4+5*y=24

Jetzt stehen auf den ersten Blick zwei Möglichkeiten zur Gleichungsumformung zu Verfügung:

beide Seiten durch 5 dividieren
bei beiden Seiten 4 subtrahieren

Lasst uns mal anschauen, was bei der ersten Möglichkeit passiert: (4+5*y)/5=24/5

Wenn wir jetzt die Klammer auf der linken Seite auflösen, erhalten wir: 4/5+y=24/5

Was nicht falsch ist, aber die Sache unnötig erschwert. Sehen wir uns die zweite Möglichkeit an, nämlich bei beiden Seiten 4 zu subtrahieren: (4+5y)-4=24-4

Lösen wir nun die Klammer auf der linken Seite auf, was in diesem Fall ein Weglassen der Klammer ist: 4+5y-4=24-4

Auf der linken Seite hebt sich 4 und -4 auf und es bleibt 5y übrig. Die rechte Seite ergibt 24 minus 4 ist gleich 20: 5y=20

Nun müssen nur noch beide Seiten durch 5 dividiert werden: 5y/5=20/5

Nun bleibt auf der linken Seite nur mehr y alleine übrig und auf der rechten Seite ergibt 20 dividiert durch 5 ist gleich 4: y=4 Damit ist die Gleichung gelöst.

Wichtig ist, dass begriffen wird, das Gleichungsumformungen immer auf beiden ganzen Seiten durchgeführt werden!

Aller guten Dinge sind drei, darum noch ein letztes Abschlussbeispiel:

Hier habe wir nun auf den ersten Blick wieder zwei Möglichkeiten zur Gleichungsumformung:

Wir subtrahieren von beiden Seiten 1 oder
wir multiplizieren beide Seiten mit 3

Oben habe ich hervorgehoben, dass es wichtig ist die Gleichungsumformungen für beide ganzen Seiten durchzuführen. Deshalb fällt der nicht der 1er auf der linken Seite weg. Es ist zwar kein Fehler auf beiden Seiten 1 zu subtrahieren, bringt uns aber für die Lösung der Gleichung nichts.

Die zweite Möglichkeit ist, beide ganzen Seiten mit 3 zu multiplizieren. Dadurch fällt auf der linken Seite das dividiert durch 3 weg. Nun muss nur mehr auf beiden Seiten 1 subtrahiert werden und man erhält z.