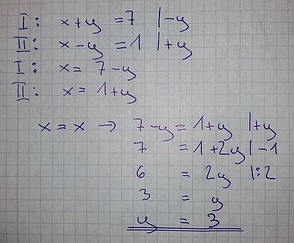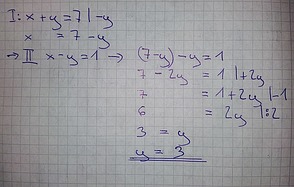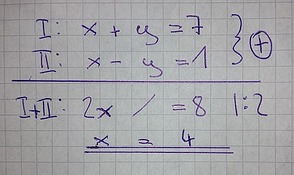Gleichungen mit zwei unbekannten Variablen lösen

ist nicht schwer. Hier lernt ihr drei verschieden Lösungsverfahren zu verstehen und anzuwenden.

Dieser Artikel zeigt euch wie ihr Gleichungssysteme mit zwei unbekannten Variablen lösen könnt. Dafür stelle ich euch die drei häufigsten Lösungsverfahren vor, wie und vor allem warum sie funktionieren. Denn wenn man versteht, warum etwas funktioniert, macht es mehr Freude in der Anwendung, man merkt es sich besser (weil es ja eh logisch ist, sobald es verstanden wurde) und man ist in der Anwendung flexibler. Deshalb ist mir es wichtig, nicht nur zu vermitteln, wie etwas funktioniert, sondern warum etwas funktioniert.

Gleichungssysteme allgemein

Um ein Gleichungssystem mit zwei unbekannten Variablen zu lösen, benötigt man zwei Gleichungen, z.B. x+y=7 und x-y=1. Nun gibt es verschiedene Verfahren um diese zwei Gleichungen mit zwei unbekannten Variablen zu lösen. Alle folglich erklärten Verfahren haben eines gemeinsam: Sie schaffen es, aus zwei Gleichungen mit zwei Variablen eine Gleichung mit einer Variablen zu machen, die dann gelöst werden kann.

Das Gleichsetzungsverfahren

Der Name verrät schon, dass etwas gleichgesetzt wird. Dazu müssen einmal beide Gleichungen auf x=…(oder y=…) umgewandelt werden:

I: x+y=7 -> x=7-y

II: x-y=1 -> x=1+y

Gleichung I sagt, dass x dasselbe ist wie 7-y

Gleichung II sagt, dass x dasselbe ist wie 1+y

Die Logik sagt, dass x dasselbe ist wie x (x=x; eh klar)

Und weil ja x einerseits 7-y ist und andererseits 1+y ist und x ja gleich x ist, ist 7-y gleich 1+y.

x=x -> 7-y=1+y

Wir setzten also gleich (Gleichsetzungsverfahren) und können die entstandene Gleichung

7-y=1+y nach y auflösen (also auf y=…umformen): y=3.

So, nun wissen wir, dass y gleich 3 ist. Das setzen wir jetzt in eine von den beiden Ausgangsgleichungen ein, um x zu erhalten. Wir setzen es in die erste Gleichung ein.

I: x+y=7 ->y eingesetzt: x+3=7 -> x=4

Das haben übrigens auch alle Verfahren gleich, dass wenn man einmal den Wert einer Variablen hat, diesen in eine der beiden Ausgangsgleichungen einsetzt, um dann den Wert der zweiten Variablen zu erhalten.

Durchstarten Mathematik: Durchstarten - in Mathematik - ...

Nur EUR 14,90

Warum Mathematik glücklich macht - 151 verblüffende ...

Nur EUR 14,95

Das Einsetzungsverfahren

Der Name verrät uns, dass hier etwas eingesetzt wird. Es funktioniert so, dass eine der beiden Gleichungen auf x=…(oder y=…) umgewandelt wird:

I: x+y=7 -> x=7-y

Weil x ja dasselbe wie 7-y ist, kann man in der zweiten Gleichung für x nun (7-y) einsetzen:

II: x-y=1 -> x eingesetzt: (7-y)-y=1 -> y=3

So, nun wissen wir, dass y gleich 3 ist. Das setzen wir wie bei allen hier vorgestellten Lösungsverfahren in eine von den beiden Ausgangsgleichungen ein, um x zu erhalten.

I: x+y=7 ->y eingesetzt: x+3=7 -> x=4

Grundlagen der Mathematik für Dummies

Mathematik für jedermann

Amazon Anzeige

Das Additionsverfahren

Um das Additionsverfahren zu verstehen, ist es wichtig, dass wir uns vor Augen führen, was Gleichungen sind, nämlich dass etwas gleich ist und zwar ist die linke Seite vom "Istgleichzeichen (=)"gleich der rechten Seite, z.B: 2+3=5. Nun kann man ja fast alles machen mit dieser Gleichung, solange man es für beide Seiten macht. So kann z.B. zu beiden Seiten 4 addiert werden, und man erhält wieder eine gültige Gleichung: 2+3+4=5+4.

Nun zum Additionsverfahren: es funktionier so, dass man beide linke Seiten der zwei Gleichungen und beide rechten Seiten der zwei Gleichungen addiert und wieder eine gültige Gleichung erhält:

I: 2+3=5

II: 2+2=4

I+II: 4+5=9

Warum darf man das machen? Warum funktioniert das?

Man darf ja bei Gleichungen alles addieren, solange man zu beiden Seiten das Gleiche addiert. Aber machen wir das? Wir haben zur linken Seite der ersten Gleichung 2+2 addiert und zur rechten Seite der Gleichung 4 addiert. Somit haben wir zwar formal nicht das Gleiche zu beiden Seiten addiert, aber wir haben das Gleiche zu beiden Seiten addiert. Es muss ja das gleiche sein, sonst wäre die zweite Gleichung keine Gleichung (linke und rechte Seite vom "Istgleichzeichen (=)" sind gleich).

Mit Gleichungen mit Variablen funktioniert das genauso. Sehen wir uns unsere zwei Gleichungen an und addieren sie:

I: x+y=7

II: x-y =1

I+II: 2x =8

Ziel beim Additionsverfahren, ist es, wie bei den anderen hier vorgestellten Verfahren aus zwei Gleichungen mit zwei Variablen eine Gleichung mit einer Variablen zu machen, was nicht immer so schnell geht, wie in diesem Beispiel. Wir werden anschließen ein realistischeres Beispiel machen, was ein wenig aufwendiger ist.

Die entstanden Gleichung kann nun nach x aufgelöst werden (x=4) und das nun in eine von den zwei Ausgangsgleichungen eingesetzt werden (wie bei den anderen Verfahren):

I: x+y=7 -> x einsetzen: 4+y=7 -> y=3

Realistischeres Beispiel

Bei diesem Beispiel muss, bevor man die Gleichungen addiert, noch etwas gemacht werden. Es müssen die Gleichungen mit Hilfe von Multiplikationen so umgeformt werden, dass wenn man sie addiert, eine Variable wegfällt. In dem Fall wurde die erste Gleichung so multipliziert, dass 6x entsteht und die zweite Gleichung wurde so multipliziert, dass -6x entsteht. Addiert man die Gleichungen nun, fällt das x weg und man erhält eine Gleichung mit einer Variablen. Diese kann dann wie gewohnt gelöst werden.