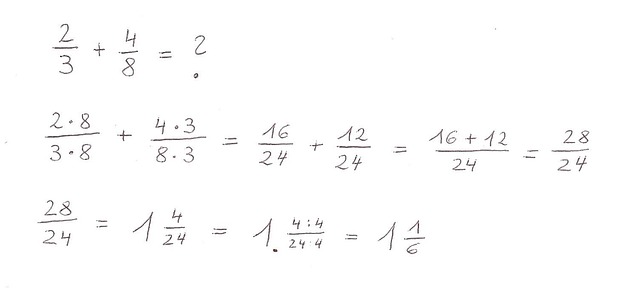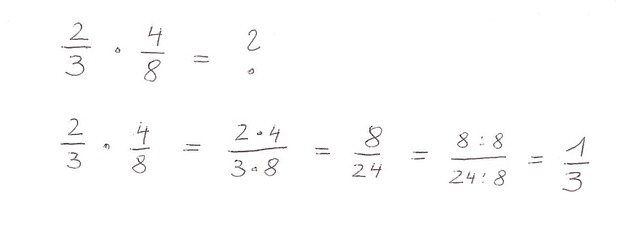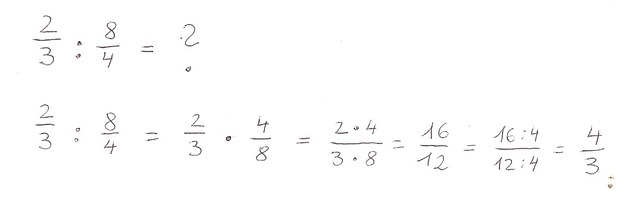Wie lernt man Bruchrechnen?

Bruchrechnen ist ein Thema, dass man nicht nur im Mathematikunterricht, sondern auch im wahren Leben braucht. Hier eine Anleitung, die jeder verstehen kann.

Ich bin weiß Gott kein Mathematikgenie, sondern bin in meiner eigenen Schulzeit in Mathematik eher verzweifelt. Genau deswegen unterrichte ich es gerne und habe sogar die Ausbildung zur mathematischen Früherzieherin gemacht. Für mich ist es absolut verständlich, wenn das Thema Mathematik nicht jeden interessiert, doch in der Regel liegt dies ganz einfach daran, dass viele Leute einfach keinen Zugang finden und nicht verstehen, warum manche, sicher nicht alle, Mathematikthemen einfach wichtig im Leben sind. So ist das auch mit Bruchrechnen. Das braucht man einfach. Die Welt besteht nicht nur aus ganzen Stücken, sondern eben auch aus Teilen. Kaum jemand kann einen ganzen Kuchen essen, sondern eben nur einen Teil. Um Bruchrechnen zu lernen, muss man die Grundlagen verstehen, dann ist es keine Hexerei!

1. Schritt: Verstehen, was ein Bruch überhaupt ist und wie man einen Bruch benennt!

Wir verwenden Brüche ganz selbstverständlich im alltäglichen Sprachgebrauch, ohne dass uns bewusst ist. Dass es beispielsweise um Brüche handelt, wenn wir eine Viertel Stunde auf jemanden warten, einen halben Liter Milch kaufen oder die Hälfte der Kinder Jungs sind.

Der Bruch ist im Prinzip ein Teil vom Ganzen. Also ein Viertel von einer ganzen Stunde, ein halber von einem ganzen Liter Milch oder die Hälfte von der ganzen Anzahl an Kindern.

Doch was bedeutet die Hälfte, ein Viertel, ein Achtel, ein Drittel, ein Sechstel oder gar zwei Viertel, drei Achtel etc....?

Das erklärt man, sofern man keine speziellen Materialien hat, am Besten mit dem guten alten Kuchen, der sich toll als Beispiel eignet. Oder man schneidet ein paar gleich große Kreise aus Papier aus, mit denen kann man Brüche auch gut zeigen, indem man sie weiter faltet oder zerschneidet. So lernt man am Einfachsten und Schnellsten, wie es zu den Benennungen der Brüche kommt.

Schneidet man einen Schokokuchen in zwei gleich große Teile, so erhält man 2 Hälften. Die 2 Hälften ergeben einen ganzen Kuchen.

Schneidet man den Kuchen in vier gleich große Teile, so erhält man 4 Viertel. Die 4 Viertel ergeben wieder einen ganzen Kuchen. Acht gleich große Teile ergeben 8 Achtel usw.

Um es danach nochmal zu verdeutlichen ist es gut, wenn man auch mit Rechtecken arbeitet. Schließlich kann man auch eckige Dinge vierteln, halbieren etc... Dann ist schon mal das Grundprinzip der Brüche schnell erlernt.

Klassische Bruchrechenkreise zum Legen von Brüchen - das perfekte Übungsmaterial für das schnelle Erlernen von Brüchen

Kasten mit Bruchrechenkreisen

2. Schritt: Verstehen, wie man den Bruch aufschreibt

Ich habe drei Stück von unserem in acht Teile geschnittenen Kuchen gegessen...... Also 3 Achtel.

Bruch (Bild: Nemo/pixabay.com)

Weiß man nun, wie ein Bruch benannt wird, so muss man lernen, wie man ihn aufschreibt. Ein klassischer Bruch besteht aus drei Teilen:

Bruchstrich: Der Bruchstrich wird in der Mitte gezogen. Er ist gleichzusetzen mit einem Divisionszeichen. 3:8=0,375: Drei Achtel Kuchen sind daher 0,375 Stück Kuchen.

Zähler: Der Zähler gibt die Anzahl der Stücke an, die uns beschäftigen. Ich habe 3 gegessen, also 3. Die Zahl steht oberhalb des Bruchstriches.

Nenner: Unter dem Bruchstrich steht der Nenner. Der gibt an in wie viele Teile der Kuchen geteilt wurde. Am Ende haben wir unseren Kuchen in 8 Teile geschnitten.

Bruchspiele zum schnelleren Verständnis

~~EUR 69,55~~ EUR 68,11

3. Schritt: Lernen, was gemischte Brüche sind, wie man kürzt, erweitert und was der Kehrwert bedeutet

Wir haben bereits gelernt, dass 8 Achtel so viel wie ein Ganzes sind, ebenso 4 Viertel, 6 Sechstel, 2 Hälften etc.... Doch als Vorbereitung zum eigentlichen Rechnen mit Brüchen muss man für die Schreibweise noch ein paar Kleinigkeiten wissen:

Manchmal muss man rechnen und hat mehr als eine ganze Zahl, also zum Beispiel möchte man wissen wie viel eineinhalb Kuchen und ein Viertel Kuchen sind. Man nennt das einen gemischten Bruch, wenn man zum Beispiel "eineinhalb" schreiben möchte. Aufgeschrieben sieht das so aus: Die Zahl 1 für das Ganze und daneben ein Halb, d.h. eine 1 im Zähler, dann der Bruchstrich und dann die 2 im Nenner.
Rechenoperationen werden in der Regel einfacher, wenn man kleinere Zahlen hat. Nachdem der Bruchstrich mit einem Divisionszeichnen gleichgesetzt werden kann, kann man einen Bruch kürzen. Statt 8 Achtel kann man auch ein Ganzes schreiben, also einfach 1, statt 4 Halbe kann man auch 2 schreiben... so weit ist das einfach. Man kann aber auch den Bruch ganz einfach in der Schreibweise ändern, wenn Zähler und Nenner gemeinsame Faktoren haben, man kann ihn kürzen. Ein Beispiel: Hat man 4 Achtel, also 4/8, so kann man sowohl 4, als auch 8 durch 4 dividieren. 4 dividiert durch 4 ergibt 1. 8 dividiert durch 4 ergibt 2. somit sind 4 Achtel genau so viel wie 1 Halb.
Für manche Rechenoperationen möchte man einen Bruch vielleicht erweitern, damit es einfacher ist, damit zu rechnen. Dafür kann man sowohl Zähler als auch Nenner einfach mit einer beliebigen Zahl multiplizieren.
Für das Rechnen mit Brüchen braucht man oft den Kehrwert. Was ist der Kehrwert? Ganz einfach... Den Kehrwert eines Bruches bekommt man, indem man Zähler und Nenner vertauscht.

Tipp: Ein tolles Gesellschaftsspiel zum Erlernen von Bruchrechnen ist das "Bruchteile Forschungslabor"

~~EUR 32,84~~ EUR 32,80

4. Schritt: Rechenoperationen mit Brüchen durchführen

Hat man nun alle Grundlagen gefestigt, mit Legematerial geübt und verstanden, worum es bei den Brüchen eigentlich geht, so kann man die Rechenoperationen angehen. Dafür muss man nur ein paar Grundregeln kennen.

Für alle Rechenoperationen gilt: Ganze Zahlen, also gemischte Brüche müssen in Bruchform gebracht werden, damit es einfacher zum Rechnen ist.
Um Brüche zu addieren oder subtrahieren muss man immer dafür sorgen, dass die Brüche den gleichen Nenner haben. Man muss sie also erweitern. Sobald das passiert ist, muss man nur mehr die Zähler addieren oder subtrahieren, um das Ergebnis zu bekommen. Beispiel: Man möchte 2 Drittel mit 4 Achtel addieren. Acht mal Drei ergibt 24, also arbeitet man am Besten mit Vierundzwanzigstel. 2 Drittel sind 16 Vierundzwanzigstel. 4 Achtel sind 12 Vierundzwangstel. 16 und 12 ergeben 28. Die Antwort ist daher 28 Vierundzwanzigstel. 28/24. Das ist keine schöne Bruchzahl, um sie als Antwort stehen zu lassen, denn sie kann noch gekürzt werden 24/24 sind ja, wie wir wissen ein Ganzes, also haben wir 1 und 4 Vierundzwangstel. 4 und 24 kann man beides durch 4 dividieren, also kürzen. Die richtige und schöne Antwort ist daher 1 1/6.

Viel einfacher ist es nun, wenn wir zwei Brüche multiplizieren möchten. Man muss einfach Zähler mit Zähler und Nenner mit Nenner multiplizieren. Beispiel: Wir multiplizieren 2 Drittel mit 4 Achtel. 2 mal 4 ist 8. 3 mal 8 ist 24. Das Ergebnis ist 8 Vierundzwanzigstel. Diese Bruchzahl kann man wieder kürzen, um ein schöneres Ergebnis zu erhalten. Man kann beide Zahlen durch 8 dividieren. 8 dividiert durch 8 ist 1. 24 dividiert durch 8 ist 3. Die schöne Antwort ist also 1 Drittel. 1/3.

Nun fehlt uns noch das Dividieren. Hier kommt nun der Kehrwert zum Einsatz. Zur Erinnerung: Den Kehrwert erhält man, wenn man Zähler und Nenner einfach vertauscht. Um zwei Brüche zu dividieren, multipliziert man einfach den ersten Bruch mit dem Kehrwert des anderen Bruchs. Beispiel: Wir wollen 2 Drittel durch 4 Achtel dividieren. Der Kehrwert von 4 Achtel ist 8 Viertel. Also multiplizieren wir 2 Drittel mit 8 Viertel, indem wir wieder Zähler mal Zähler und Nenner mal Nenner nehmen. 2 mal 8 ist 16. 3 mal 4 ist 12. Die Antwort ist 16 Zwölftel. Das kann man natürlich wieder kürzen, denn Zähler und Nenner kann man beide durch 4 dividieren. 16 durch 4 ergibt 4. 12 durch 4 ist 3. Die schöne gekürzte Antwort ist 4 Drittel. 4/3.