Boxplot interpretieren

Whisker, Median, Quantil bzw. Quartile zeigt das Boxplot an

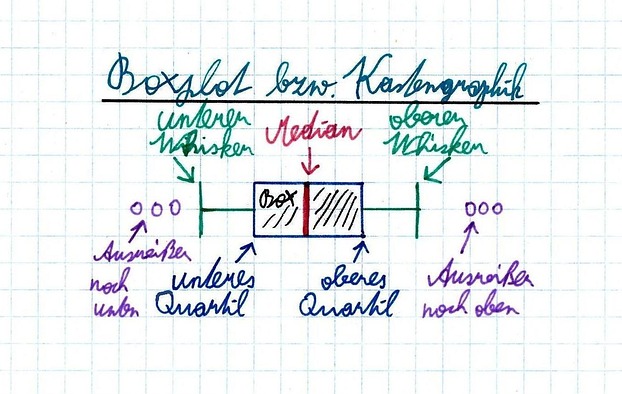
Die fünf genannten Werte sind der obere und untere Whisker, der Median sowie das 25-Prozent-Quantil (=unteres Quartil) und 75-Prozent-Quantil (=oberes Quartil). Die schwarz schraffierte Box mit blauem Rand enthält demnach 50% der Fälle der Stichprobe und wird Quartilsabstand genannt, da sie den Abstand vom oberen und unteren Quartil misst. Innerhalb der Box liegt der Median.

1. Der obere Whisker zeigt den höchsten Wert der Variable an, der noch innerhalb der Norm liegt.
2. Der untere Whisker zeigt dementsprechend den niedrigsten Wert an, der noch innerhalb des Normbereichs liegt.
3. Der Median teilt die Stichprobe genau in der Mitte in zwei Hälften. Das heißt 50 Prozent der Fälle der Stichprobe weisen Werte bis zur Höhe des Median auf.
4. Das 25-Prozent-Quantil, auch unteres Quartil genannt, teilt wie der Median die Stichprobe in zwei Teile. 25 Prozent der Fälle der Stichprobe liegen unterhalb des 25-Prozent-Quantil und 75 Prozent der Fälle darüber.
5. Das 75-Prozent-Quantil, auch oberes Quartil genannt, ist fast genauso wie das 25-Prozent-Quantil mit dem Unterschied, dass 75 Prozent der Fälle unterhalb des 75-Prozent-Quantils liegen und 25 Prozent darüber. Mit anderen Worte zeigt das 25-Prozent-Quantil die Grenze zum unteren Viertel der Fälle an und das 75-Prozent-Quantil das obere Viertel der Fälle.

Werte, die außerhalb der Whiskers liegen, werden als Ausreißer nach unten bzw. nach oben bezeichnet. Sofern die Werte mehr als 3 Boxlängen vom 25-Prozent-Quantil bzw. 75-Prozent-Quantil entfernt liegen, werden als Extremwerte bezeichnet und damit in der Regel nicht in die Analyse miteinbezogen, da sie die Auswertung verzerren und das Ergebnis verfälschen würden.

Boxplots interpretieren einfach gemacht

Die fünf oben genannten Werte stellen quasi das Alphabet des Boxplots dar und als nächsten Schritt werden aus den Buchstaben, Median, Whisker, Quartile bzw. Quantile die ersten Sätze gebildet. Die folgenden Bilder zeigen quasi den Normalfall von Boxplots an, wie sie in der Natur vorkommen. Zwei neue Begriffe in diesem Zusammenhang sind die Schiefe und Kurtosis.

• Schiefe: Die Schiefe ist eine statistische Kennzahl, die angibt, in welche Richtung die Stichprobe verteilt ist. Es wird unterschieden zwischen rechtsschief und linksschief. Wenn etwas rechtsschief ist, dann ist es zugleich linkssteil, und wenn etwas linksschief ist, dann ist es rechtssteil. Linksschief bzw. rechtssteil bedeutet Daumen mal PI, dass der Median sich auf der eher linken Seite in der Box befindet und die Box, als Gesamtes eher näher dem linken Whisker ist, als dem rechten Whisker.
• Kurtosis: Die Kurtosis, auch Wölbung genannt, gibt die Krümmung bzw. Steilheit der Verteilung der Fälle in der Stichprobe an. Ist die Krutosis flachgipfelig, dann sind die Fälle stark unterschiedlich verteilt. Ist die Kurtosis spitzgipfelig, dann sind die Fälle der Stichprobe in einem kleinen Bereich konzentriert. Beim Boxplot erkennt man eine spitze Kurtosis daran, dass die Box sehr schmal ist (kleiner Interquartilsabstand) und eine flache Kurtosis daran, dass die Box sehr breit ist, also eine relativ großen Interquartilsabstand hat. Sehr breit bedeutet, dass die Box eine große Fläche, mehr als die Hälfte der Fläche zwischen den Wiskern, einnimmt.

Das obige Beispielbild zeigt eine perfekte Normalverteilung an. Die Box nimmt genau die Hälfte der Fläche zwischen den Whiskern ein und ist demnach weder flachgipfelig noch spitzgipfelig von der Kurtosis her. Des Weiteren ist der Median genau in der Mitte der Stichprobe zu finden und die Box befindet sich genau zwischen beiden Whiskern. Demnach ist die Verteilung weder linkssteil bzw. rechtsschief noch rechtssteil bzw. linksschief. Alles ist genau in der Mitte und gleich verteilt. Dies kommt in der Realität nicht vor.

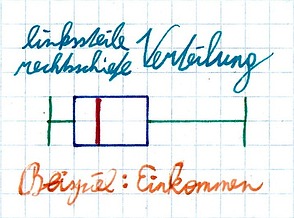
Rechtsschiefe bzw. linkssteile Verteilung beim Boxplot

Ein Beispiel für eine rechtsschiefe bzw. linksschiefe Verteilung wäre das Einkommen. Rund drei Viertel der Arbeitnehmer arbeiten Vollzeit und nur rund ein Viertel ist Teilzeit angestellt. Dementsprechend ist die Box eher auf der linken Seite und auch der Median auf der linken Seite zu finden. Das Beispielbild zeigt eine typische rechtsschiefe bzw. linkssteile Verteilung, da:

1. Der Median auf der linken Seite zu finden ist.
2. Die Box auf der linken Seite zu finden ist.
3. Das untere Quartil ist näher zum linken Whisker als das obere Quartil zum rechten Whisker.

Mit anderen Worten: Die Stichprobe ist rechtsschief bzw. linkssteil verteilt. Im Falle des Einkommens ließe sich dies so interpretieren, dass der Großteil der Fälle weniger als den Durchschnittswert des Einkommens in Österreich verdient, da der Median auf der linken Seite zu finden ist. Die Kurtosis ist eher spitz, was bedeutet, dass ein überdurchschnittlich großer Teil der Fälle annähernd dasselbe Einkommen verdient und die Streuung der Verteilung relativ gering ist. Mit einem Satz: Die meisten Fälle der Stichprobe haben ein Einkommen, das unter dem Durchschnitt liegt und überdurchschnittlich viele Fälle in der Verteilung verdienen annähernd das gleich Einkommen.

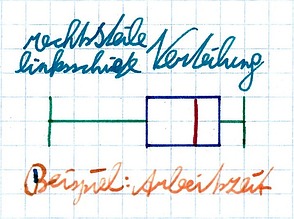
Linksschiefe bzw. rechtssteile Verteilung beim Boxplot

Hier ist genau das Gegenteil zum oben Genannten zu sehen. Alle markanten Punkte sind auf der rechten Seite der Box zu sehen. Hier nun wiederum die Checkliste:

1. Der Median ist auf der rechten Seite zu finden.
2. Die Box ist auf der rechten Seite zu finden.
3. Das obere Quartil ist näher zum rechten Whisker als das linke Quartil zum linken Whisker.

In dem fiktiven Beispiel würde es bedeuten, dass die Hälfte der befragten Personen mehr Stunden als den Durchschnittswert arbeiten, was man in die Richtung interpretieren kann, dass weniger Personen Teilzeit als Vollzeit arbeiten. Ebenso ist die Verteilung wieder spitzgipfelig, was bedeutet, dass ein überdurchschnittlich großer Anteil der Personen eher die gleiche Stundenzahl arbeitet.

Boxplot ist nicht gleich Boxplot

Im Endeffekt ist in der Statistik vieles Argumentationssache und die Übergänge sind fließend. Die oben gezeigten Beispiele sind eindeutige rechts- oder linksschiefe Verteilungen. In der Realität hat man es oft mit solchen Boxplots zu tun, wo man nicht auf den ersten Blick erkennen kann wie die Wölbung, Schiefe usw. gestaltet ist. Bei den Beispielen wurden gezielt keine Zahlenwerte genannt, da es bei Verteilungen um Verhältnisse geht und um die Gestalt der Verteilung.