Die wunderbare Welt der Quantenphysik: Verschränkte Teilchen und Quantencomputer

Verschränkte Teilchen, die normale Welt und das Doppelspaltexperiment

Stellen Sie sich vor, sie kennen zwei Bekannte, die an zwei unterschiedlichen Orten wohnen und nicht miteinander kommunizieren können. Jeder besitzt eine Schatulle, in der sich jeweils eine schwarze und eine weiße Kugel befindet. Jeden Tag schicken sich die Beiden die Schatullen zu, öffnen die Schatullen zu einer verabredeten Zeit und nehmen mit verbundenen Augen jeweils eine Kugel heraus. Danach werden die Schatullen weggeworfen, denn zur Spielregel gehört, dass man in die Schatullen nicht hineinsehen darf.

Das Erstaunliche ist nun: Egal wie oft das Spiel wiederholt wird, beide ziehen aus einem unbekannten Grund immer zwei Kugeln gleicher Farbe. Alle rätseln, wie das geschehen kann, denn  beide schwören, keinen geheimen Trick anzuwenden und sich nicht insgeheim zu verabreden!

Dieses Verhalten gibt es tatsächlich!!!

In der Welt der Quanten ist dieses Phänomen tatsächlich zu beobachten - und zwar mit verschränkten Photonen oder anderen verschränkten Elementarteilchen. Schauen wir uns das ganze mit Photonen an: Zunächst werden zwei verschränkte Photonen erzeugt, die voneinander wegfliegen. Nun wird in den Weg jedes Photons ein horizontal ausgerichteter Polarisationsfilter gestellt. Im Prinzip kann jedes Photon durch seinen Polarisationsfilter durchgelassen oder von ihm absorbiert werden. Aber beide Photonen verhalten sich wie im Beispiel oben immer gleich: Entweder werden beide durchgelassen oder beide absorbiert - so als ob Sie durch eine geheimnisvolle Kraft voneinander wüssten!

Selbst Einstein wollte das nicht glauben

Da das Phänomen so unglaublich erscheint und unserer Intuition völlig widerspricht, hatte auch Einstein Zweifel an dieser seltsamen Fernwirkung. Er postulierte deshalb so genannte lokale verborgenen Variablen, die das Phänomen auf uns verständliche Weise erklären. Übertragen auf das Beispiel mit den Schatullen hiese dies, dass z.B. ein Beamter auf dem Postamt die Schatullen öffnet und in jede Schatulle eine Kugel gleicher Farbe legt. Da die Schatullen ja nach Entnahme einer Kugel weggeworfen werden, ist von Seiten der Adressaten nicht zu überprüfen, ob die Schatullen manipuliert wurden.

Doch auch dieser Einwand konnte durch aufwendige Experimente widerlegt werden. Die Idee zur Wiederlegung dieses Einwands hatte John Bell in den 1960er Jahren. Bekannt unter dem Namen Bellsche Ungleichung wurde der Beweis durch Alain Aspect im Jahre 1982 experimentell erbracht.

Das Rätsel bleibt bestehen

Es sieht also ganz so aus, als würden die zwei Kugeln auf irgendeine rätselhafte Art ihr Verhalten aufeinander abstimmen, und zwar erst dann, wenn die beiden Bekannten ihre Schatullen öffnen. Durch dieses nicht erklärbare Verhalten ist die Diskussion um die Deutung der Quantentheorie nie zum Stillstand gekommen. Deshalb werden auch heute noch Theorien mit verborgenen Variablen (die dann allerdings nichtlokal sein müssen) entwickelt, um die Quantenphysik intuitiv zu fassen.

Allerdings hat Anton Zeilinger - ein österreichischer Quantenphysiker der Universität Wien - bereits Experimente veröffentlicht, die eine realistische Interpretation der Quantenmechanik unmöglich machen. Weitere Informationen zu diesen Experimenten sind in dem Artikel An experimental test of non-local realism zu finden.

Das berühmte Doppelspaltexperiment und der Welle-Teilchen-Dualismus

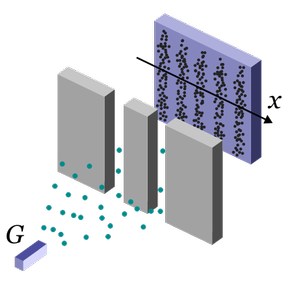Jeder, der sich mit der Quantenphysik beschäftigt, erfährt sehr schnell vom berühmten Doppelspaltexperiment: Man lässt kohärentes, monochromatisches Licht durch eine Blende mit zwei schmalen, parallelen Schlitzen auf einen dahinter liegenden Beobachtungsschirm treten und beobachtet ein Interferenzmuster.

Den gleichen Effekt kann man erreichen, indem man einen Stein ins Wasser wirft und die Wellen beobachtet, die ein entsprechendes Hindernis passieren. Das heißt also, die Lichtteilchen - auch Photonen genannt - verhalten sich im Doppelspaltexperiment wie eine Welle. Aber nicht nur die Photonen zeigen dieses Verhalten, das Experiment kann auch mit Elektronen, Neutronen, Atomen oder sogar mit Molekülen durchgeführt werden. So hat z.B. im Jahre 1961 Claus Jönsson den Wellencharakter von Elektronen nachgewiesen.

Kurioserweise verhalten sich diese Materiebausteine aber nicht immer wie Wellen, sondern manchmal eben auch wie Teilchen. Nehmen wir an, wir werfen beliebig oft Bälle durch die zwei Spalten, so ergibt sich anschließend kein Interferenzmuster, sondern es werden - wie aus der klassichen Physik bekannt - zwei Peaks direkt hinter den Spalten entstehen. Die physikalische Messung beeinflusst in diesem Fall nicht das Ergebnis.

Erstaunlicherweise tritt dieser Effekt nicht nur ein, wenn ein Spalt abgedeckt wird, sondern auch dann, wenn man herausfinden möchte, welchen der beiden Wege das Photon genommen hat. Misst man also die Photonen vor der Durchquerung, verschwindet das Interferenzmusters. Ohne Messung hingegen bleibt das Muster erhalten und die Photonen nehmen quasi beide Wege gleichzeitig.

Auch die Anzahl der Photonen oder der zeitliche Ablauf spielen bei der Durchführung des Experiments keine Rolle: Bei einer langsamen Folge von einzelnen Teilchen baut sich das Interferenzmuster allmählich auf. Und das ist nun wirklich überraschend, denn jedes einzelne Teilchen kennt ja die früher oder später kommenden Teilchen nicht und passiert daher die Spalten unabhängig von den anderen. Daher muss auch die Interferenz - also die Verteilung der Wahrscheinlichkeit des Ankommens an den Positionen auf der Photoplatte - bei jedem einzelnen Durchflug entstehen: jedes Teilchen interferiert scheinbar mit sich selbst.

Als Erklärung für dieses Verhalten hat sich die Kopenhagener Deutung am meisten etabliert: Man sagt, dass die Teilchen alle Spalten gleichzeitig durchqueren und sich dabei in einer sogenannten Superposition aller möglichen Wege befinden. Mehrere dieser Wege können nun miteinander interferieren und so das erwartete Interferenzmuster bilden. Der Detektor - also die Photoplatte - misst in diesem Fall aber immer nur ein Teilchen und legt damit die Positionen der Photonen erst nach dem Durchflug fest. Findet die Detektion hingegen schon vor dem Spalt statt, so stehen nicht mehr alle Wege für die Interferenz zur Verfügung. Damit ergibt sich eine andere Verteilung auf der Photoplatte und das Interferenzmuster verschwindet.

Quantencomputer und Qubits - Kann ein Quantecomputer mehr berechnen als ein herkömmlicher Computer?

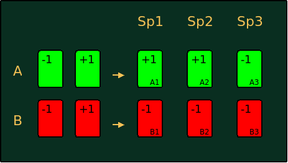Ja, er kann. Was er alles kann, soll mit dem Quantenspiel erklärt werden. Das Quantenspiel wird mit 3 Spielern gespielt, die in jeder Runde aus zwei grünen (A) und zwei roten Karten (B) auswählen dürfen. Die Karten sind jeweils mit -1 und +1 beschriftet. Vor jeder Runde dürfen sich die Spieler beraten und eine Strategie ausdenken. Am Ende des Spiels zählen nicht die einzelnen Antworten der Spieler, sondern es wird ein Produkt aus den Antworten gebildet, wobei folgende Kombinationen zum Gewinn führen:

• Wird nach den Antworten A1, A2 und A3 gefragt, muss das Produkt -1 ergeben
• Wird nach den Antworten A1, B2 und B3 gefragt, muss das Produkt +1 ergeben
• Wird nach den Antworten B1, A2 und B3 gefragt, muss das Produkt +1 ergeben
• Wird nach den Antworten B1, B2 und A3 gefragt, muss das Produkt +1 ergeben

Das Diagramm zeigt ein Beispiel, bei dem die Spieler 1 und 2 die grüne Karte mit der Beschriftung +1 und die rote Karte mit der Beschriftung -1 gewählt haben, Spieler 3 hingegen hat beide Karten mit der Beschriftung -1 gewählt. In diesem Beispiel hätten die Spieler

• im ersten Fall gewonnen, denn A1 * A2 * A3 = (+1) * (+)1 * (-1) = -1
• im zweiten Fall gewonnen, denn A1 * B2 * B3 = (+1) * (-1) * (-1) = +1
• im dritten Fall gewonnen, denn B1 * A2 * B3 = (-1) * (+1) * (-1) = +1
• aber im vierten Fall verloren, denn B1 * B2 * A3 = (-1) * (-1) * (-1) = -1

Die Frage ist nun, ob es für die Spieler eine Strategie gibt, bei der sie immer gewinnen. Die Antwort latuet "Nein" und kann mit einer einfachen Überlegung und ein bischen Mathematik gezeigt werden. Betrachten wir hierzu zunächst die letzten 3 Gewinnfälle, bei denen das Ergebnis immer +1 sein muss: Da

A1 * B2 * B3 = B1 * A2 * B3 = B1 * B2 * A3 = +1 gilt, muss auch

(A1 * B2 * B3) * (B1 * A2 * B3) * (B1 * B2 * A3) = +1 gelten. Nach Ausmultiplizieren erhalten wir

A1 * A2 * A3 * B1² * B2² * B3² = +1. Dies wiederum führt zu

A1 * A2 * A3 * +1 * +1 * +1 = +1, also folgt

A1 * A2 * A3 = +1. Und dies steht im Widerspruch zum ersten Gewinnfall, bei dem ja

A1 * A2 * A3 = -1 gelten muß!

Werden nun Photonen verschränkt, kann ein Experiment aufgebaut werden, das dieselbe logische Struktur aufweist, wie das Quantenspiel. Dabei schaffen es die Photonen auf rätselhafte Weise immer zu gewinnen und legen eine "ausgeklügeltere" Strategie an den Tag als unsere menschlichen Mitspieler. Wie die Photonen das machen ist unbekannt, aber Experimente zeigen, dass es funktioniert.

Können Quantencomputer realisiert werden?

In der heutigen Zeit gibt es einige Vorschläge, wie Quantencomputer realisiert werden können. So wurden im Labor bereits einige dieser Konzepte erprobt und auch Quantencomputer mit wenigen Qubits gebaut. Von einer tatsächlichen Anwendung und praktischem Nutzen ist man aber noch weit entfernt, so dass der Quantencomputer im Moment eher ein theoretisches Konzept darstellt.

Die Funktionsweise eines Quantencomputers beruht auf Qubits, wobei ein Qubit ein beliebig manipulierbares Zweizustands-Quantensystem darstellt. So kann durch die Verschränkung eines Satzes von n Qubits ein beliebiger Satz von Sequenzen n klassischer Bits gleichzeitig dargestellt werden. Beispielsweise kann man mit 4 Qubits einen Zustand herstellen, der genau die Bitfolgen 0000, 0101, 1011 und 1110 enthält und keine anderen. Im Extremfall sind alle 2⁴ = 16 möglichen Bitfolgen darin enthalten, also die Folgen 0000, 0001, 0010 bis hin zu 1111. Ein entsprechend präpariertes Quantenbyte - bestehend aus 8 Qubits - könnte daher 2⁸ = 256 Bitfolgen auf einmal speichern.

Das erstaunliche an den Quantecomputern ist nun, dass sie Operationen auf allen Bitfolgen gleichzeitig ausführen können. Herkömmliche Computer müssten die Operationen sequentiell - also nacheinander - für durchführen.

Doch auch beim Quantencomputer gibt es Nachteile: Ein Problem ist, dass jede Messung ein zufälliges Ergebnis liefert. Man kann sich das gewünschte Resultat also nicht einfach aus der Ergebnismenge herauspicken. Dafür muss man zusätzliche spezifische quantenmechanische Transformationen durchführen, die genau einem Bitmuster entsprechen und mehrere Bitmuster durch Überlagerungen ineinander überführen können.

Weiterhin ist auch ein so erhaltenes Ergebnis nur mit einer gewissen Wahrscheinlichkeit "richtig". Deshalb müssen entsprechende Berechnungen öfters wiederholt werden, um eine statisch signifikante Aussage treffen zu können.

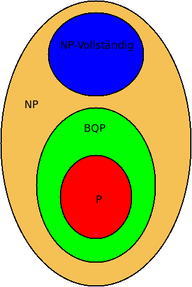
Noch ein letztes Wort für die theoretischen Informatiker: Mit Quantencomputern lassen sich einige der nichtdeterministisch-polynomialen (NP) Probleme in polynomialer Zeit lösen, wie die Algorithmen von Grover- und Shor zeigen (BQP-Probleme). So können mit dem Algorithmus von Shor große Zahlen auf einem Quantencomputern in polynomieller Zeit in ihre Faktoren zerlegt werden. Der Algorithmus ist aber speziell auf das Faktorisieren von Zahlen zugeschnitten und lässt sich daher nicht auf andere NP-Probleme übertragen. Es ist trotzdem nicht ausgeschlossen, dass noch weitere Spezialfälle in NP gefunden werden, die sich mit speziellen Quantenalgorithmen effizient lösen lassen. Doch leider ist bis heute kein Ansatz für einen Quantenalgorithmus erkennbar, der bei allen NP-Problemen greift. Es bleibt also weiterhin spannend - auch auf diesem Gebiet.

So, ich hoffe, ich habe Euer Interesse an der wunderbaren, aber seltsamen Quantenwelt wecken können. Jedenfalls bin ich sehr gespannt, welche weiteren genialen Entdeckungen im Laufe der Zeit auf uns warten :-)