Median berechnen

Median berechnen bei einer ungeraden Stichprobe

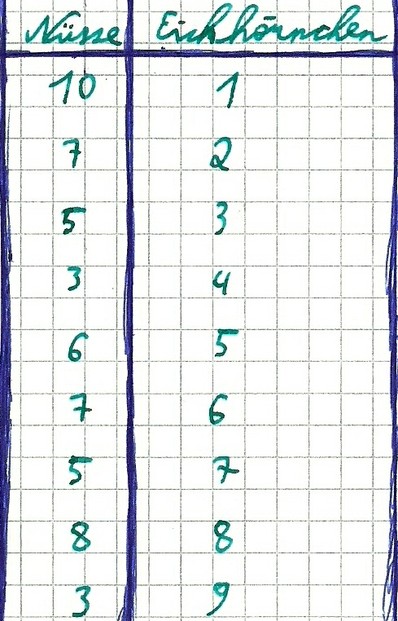
Da hier der geringste Rechenaufwand besteht und der Mensch von Natur aus faul ist, beginne ich mit diesem Beispiel. Ich habe im Wald neun Eichhörnchen entdeckt und jedes hatte eine unterschiedliche Anzahl Nüsse gesammelt. Der erste Schritt ist, dass man die Eichhörnchen nach der gesammelten Nussanzahl in aufsteigender Anzahl ordnet. Die wenigsten Nüsse, jeweils 3 Stück, haben Eichhörnchen 4 und 9 gesammelt und bekommen deswegen den Index x1 bzw. x2 zugeordnet. 5 Nüsse haben die Eichhörnchen 3 und 7 gesammelt diese bekommen den Index x3 und x4 zugeordnet. Das Eichhörnchen 5 hat 6 Nüsse gesammelt und kriegt den Index x5. Jeweils 7 Nüsse haben die Eichhörnchen 2 und 6 gesammelt und werden mit dem Index x5 und x6 markiert. Das Eichhörnchen 8 hat 8 Nüsse gesammelt und erhält den Index x8. Ein Eichhörnchen mit Nummer 1 hat sogar 10 Nüsse gesammelt und erhält deshalb Index x9. Insgesamt haben wir 9 Eichhörnchen also hat unsere Stichprobe die Größe n=9 und die Indizes x1=3, x2=3, x3=5, x4=5, x5=6, x6=7, x7=7, x8=8, x9=10. Jetzt muss nur noch in die Formel eingesetzt werden und der Median ist berechnet! (n+1)/2=(9+1)/2=5 also ist der Median beim Index x5 und x5=6 Nüsse. Der Median liegt also bei x0.5=x~=6 Nüssen. Genau die eine Hälfte der Eichhörnchen hat weniger als 6 Nüsse gesammelt und die andere Hälfte hat mehr als 6 Nüsse gesammelt.

Median berechnen bei klassierten Daten

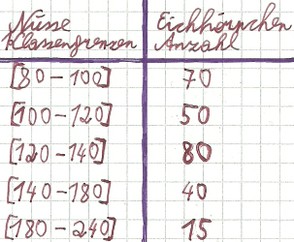
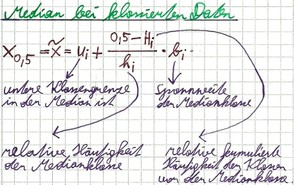
Bei klassierten Daten ist der Median bzw. Zentralwert zwar ein wenig schwieriger zu berechnen, aber wenn man die Formel als Geschichte definiert, dann ist es auch keine Hexerei. In Worten ausgedrückt lautet die Formel: Die untere Klassengrenze in der der Median gelegen ist plus Klammer auf 0.5 minus der relativen kumulierten Häufigkeit der Klassen vor der Medianklasse Klammer zu geteilt durch die relative Häufigkeit der Medianklasse multipliziert mit der Spannweite der Medianklasse. Zuerst berechnet man die Klasse in der der Median vorkommt. Alle Eichhörnchen werden zusammengezählt und durch 2 geteilt. n/2=(70+50+80+40+15)/2=127,5 also muss der Median in der dritten Klasse vorkommen da irgendwo innerhalb der dritten Klasse die Stichprobe sich in 2 Hälften teilt. Nun geht es Schlag auf Schlag beim Median berechnen. Untere Klassengrenze ui=120, Spannweite bi=20, relative Häufigkeit der Medianklassen hi=80/n=80/255=~0,31, relative kumulierte Häufigkeit der Klassen vor der Medianklasse Hi=(70+50)/n=(70+50)/255=~0,47. Damit wären alle Angaben gemacht und man muss zum Median berechnen nur noch die Formel einsetzen.

x0.5=x~=ui+(0.5-Hi)/hi*bi=120+(0.5-0.47)/0.31*20=121,94 womit der Median bei 121,94 liegt.