Mittelwert berechnen

Das arithmetische Mittel

Ein gutes Beispiel für die Berechnung des arithmetischen Mittel wäre die Errechnung des durchschnittlichen Gewichts einer Kartoffel. Christian der Statistiker ist nur wenig praktisch veranlagt und möchte sich Kartoffelpüree kochen und im Rezept steht, dass man für eine Portion Kartoffelpüree 5 durchschnittliche Kartoffeln benötigt. Er hat aber insgesamt 10 Kartoffeln zu Hause und er weiß nicht, wie schwer eine durchschnittliche Kartoffel ist.

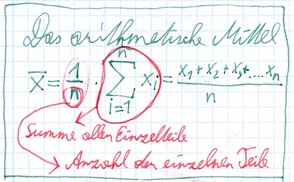
Da er Statistiker ist, errechnet er sich das durchschnittliche Gewicht einer Kartoffel mit der oben beschriebenen Formel. Zuerst wiegt der die 10 Kartoffeln ab und erhält dadurch seine Werte x1, x2, x3 bis x10 wobei jedes einzelne x für das Gewicht einer einzelnen Kartoffel in beliebiger Reihenfolge steht. Er erhält folgende Werte x1=30, x2=35 x3=50, x4=25, x5=60, x6=55, x7=80, x8=75, x9=35, x10=40.

Da er insgesamt 10 Kartoffeln gewogen hat, ist die Anzahl n also n=10 und damit kann er in die Formel einsetzen:(x1+x2+x3+....xn)/n=(30+35+50+25+60+55+80+75+35+40)/10=485/!=48,5. Damit kann er nun sein Kartoffelpüree kochen, da er nun weiß, dass das arithmetische Mittel des Gewichts einer seiner Kartoffeln 48,5 ist.

Das arithmetische Mittel, auch Mittelwert genannt, gibt immer den Durchschnittswert bezogen auf die Stichprobe an und darf nur bei metrischen Datenniveau verwendet werden. Er ist sehr anfällig auf extreme Werte, sogenannte Ausreißer.

Kleines Detail am Rande: Obwohl man gerne vom Notendurchschnitt redet, ist es statistisch falsch! Da die Notenskala keine metrisches Datenniveau darstellt sondern nur ordinales Datenniveau aufweist. Die Noten sind nur Ordinal, da die Abstände zwischen einer Eins und einer Fünf nicht genau gleich sind.

Das gewichtete Mittel

Hier bietet sich als Beispiel ein Lager mit verschiedenen Sorten von Kartoffeln an. Christian hat das Kartoffelpüree so gut geschmeckt, dass er sich nun sogar ein Lager mit verschiedenen exotischen Kartoffelsorten angelegt hat. Von den roten Kartoffeln hat er 75 Kilo gekauft zu einem Preis von 5 Euro pro Kilo, von den blauen Kartoffeln hat er 65 Kilo gekauft zu einem Preis von 3 Euro pro Kilo, von den grünen Kartoffeln hat er 85 Kilo gekauft zu einem Preis von 2 Euro pro Kilo. Nun stellt er sich die Frage, wie viel er durchschnittlich für ein Kilo Kartoffeln im Lager bezahlt hat? Diese Frage beantwortet er sich mit der Formel für das gewichtete Mittel, von der es zwei Berechnungsvarianten gibt. Die Variante ist die meiner Meinung nach einfachere Berechnungsweise:

Variante 1: (75 Kilo * 5 Euro + 65 Kilo * 3 Euro + 85 Kilo * 2 Euro) / (75 + 65 + 85) =  ~3.29 Euro

Die zweite Variante  berechnet sich über die relativen Häufigkeiten und den Durchschnittspreisen:

Variante 2: Die Formel für relative Häufigkeit ist => Teilmenge geteilt durch Gesamtmenge. Relative Häufigkeit für rote Kartoffeln 75/(75+65+85)=~0,33, die relative Häufigkeit für blaue Kartoffeln 75/225=~0,29, und die relative Häufigkeit für grüne Kartoffeln 85/225=~0,38.

Eingesetzt in die Formel ergibt dies 0,33*5+0,29*3+0,38*2=~3,29 Euro.

In Worten ausgedrückt heißt dies, dass Christian durchschnittlich 3,29 Euro für jedes Kilo Kartoffeln in seinem Lager bezahlt hat.

Das Einsatzgebiet des gewichteten Mittels ist immer dort, wo verschiedene Mittelwerte und verschiedene Teilmengen vorhanden sind und der Durchschnittswert der Gesamtmenge berechnet werden muss.

Das geometrische Mittel

Inzwischen ist Christian Leidenschaft für Kartoffeln so gewachsen, dass er sogar Kartoffeln an der Börse handeln will. Da ihm die blauen Kartoffeln nicht schmecken, will er sie an der Börse verkaufen. An der Börse findet er die Preisentwicklung für blaue Kartoffeln folgendermaßen vor.[2020: +5%] [2021: -12.5%] [2022: +20%] [2023: +3%] [2024: -4%] [2025: -2,5%]

Nun stellte sich die Frage wie sich der Preis entwickelt hat zwischen 2020 und 2025? Christian denkt sich, kein Problem, das schaffe ich mit dem geometrischen Mittel.

Der erste Schritt ist es, die  Prozente im richtigen Format hinzuschreiben:

Wenn der Preis steigt, ist Formel 1+p/100=1+5/100=1+0,05=1,05 für das Jahr 2020, im Jahr 2021 gab es einen Verlust, und wenn der Preis sinkt, gilt die Formel 1-p/100=1-12,5/100=0,875, im Jahr 2022 stieg der Preis wieder um 20% 1+20/100=1,20, das Jahr 2023 brachte einen Anstieg um 3% 1+3/100=1,03, im Jahr 2024 wieder ein Verlust von 4% 1-4/100=0,96 und 2025 folgte wieder ein Preisverfall von 2,5% 1-2,5/100=0,975.

Der nächste Schritt ist in die Formel einsetzen:

xgeo=(x1*x2*x3....xn)^(1/n)=(1,05*0,875*1,2*1,03*0,96*0,975)^(1/6)=1,01 was bedeutet, dass der Preis in 6 Jahren um 1 Prozent gestiegen ist, da die Formel (xgeo-1)*100 den Prozentwert angibt, um den der Wert im Zeitverlauf gestiegen bzw. gesunken ist.

Die Moral von der Geschichte ist, dass Christian nun weiß, dass der Kartoffelpreis im Zeitraum von 2020-2025 durchschnittlich um 1 Prozent gestiegen ist, obwohl es innerhalb des Zeitraums zu ordentlichen Preisschwankungen kam.

Kontrolle: Einfach eine fiktive Zahl annehmen sagen wir 100 und nachrechnen 100*1,05*0,875*1,2*1,03*0,96*0,975=~106,29 und 100*1,01^6=~106,28 passt! (Es kommt durch das Runden zu einem minimal unterschiedlichen Ergebnis.)