Statistik: Ein Histogramm zeichnen ist keine Hexerei
Hier wird anhand eines Beispiels erklärt, wie ein Histogramm von Hand gezeichnet wird. Die Handhabung unterschiedlicher Klassenbreiten wird ebenso berücksichtigt.Schritt 1: Klassenbreiten berechnen.
Die Klassenbreiten bi berechnet man, indem man die obere Klassengrenze hernimmt und die untere Klassengrenze abzieht. In unseren Fall wäre das 1000-750 = 250, 1250-1000 = 250, 1500-1250 = 250 und zu guter Letzt 2000-1500 = 500. Die letzte Klassenbreite weicht von den anderen ab, worin ein kleiner Hund begraben liegt, auf den ich später noch zurückkommen werde, um ihn auszugraben.
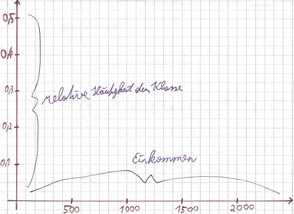
Angabe zum Histogramm
Schritt 2: Die relativen Häufigkeiten berechnen.
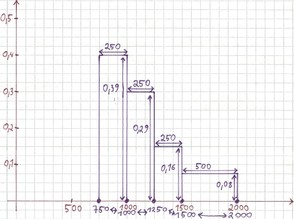
Die relativen Häufigkeiten hi berechnet man, indem die Gesamtzahl der Fälle n ausrechnet und danach die Anzahl der Fälle in jedem einzelnen Intervall durch die Gesamtzahl der Fälle dividiert. In unserem Fall sind die Fälle die Anzahl der Personen. 100 + 75 + 40 + 40 = 255, 100/255 = 0,39, 75/255 = 0,29, 40/255 = 0,16 und 40/255 = 0,16. Eine Kontrolle ist, dass alle relativen Häufigkeiten zusammen die Ziffer eins ergeben müssen. 0,39 + 0,29 + 0,16 + 0,16 = 1 so weit, so gut.
Koordinatensystem Histogramm
Schritt 3: Koordinatensystem zeichnen und definieren.
Die relativen Häufigkeiten hi bilden Höhe auf der Y-Achse und das Einkommen in Klassen wird auf der X-Achse abgebildet. Hierbei ist zu beachten, dass die Maßstäbe und Dimensionen des Koordinatensystems so gewählt werden, dass einerseits genug Platz für das Histogramm vorhanden ist und andererseits das Histogramm übersichtlich und anschaulich dargestellt wird.
Schritt 4: letzte Überprüfung vor dem Zeichenwerk
Die relativen Häufigkeiten hi bilden die Höhe und die Klassengrenzen jeweils die unteren Eckpunkte der Flächen des Histogramms auf der X-Achse. Jetzt wird allerdings der vorhin begrabene Hund wieder ausgegraben. Die Flächentreue des Histogramms darf nicht verletzt werden, da die Klassenbreite der letzten Klasse sich von der der anderen Klassen unterscheidet.
Die Klassenbreite der letzten Klasse ist mit dem Wert fünfhundert doppelt so groß, wie die der anderen Klassen deren Breiten nur dem Wert zweihundertfünfzig betragen. Die Lösung liegt darin, dass die "Höhe" der Klassen im Verhältnis zur Klassenbreite angepasst wird. Fünfhundert geteilt durch zweihundertfünfzig ergibt zwei, also ist das Verhältnis zu den anderen Klassen zwei zu eins. Dadurch ist die "Höhe" der vierten Klasse nur 0,8, da 0,16/2 = 0,08. Dadurch bleibt die Flächentreue des Histogramms gewährt, da die größere Klassenbreite durch geringere "Höhe" ausgeglichen wird.
Schritt 5: Das Histogramm wird zu Papier gebracht.
Das Lineal wird angesetzt und das Koordinatensystem gezeichnet, wobei zu beachten ist, dass die relativen Häufigkeiten zusammen maximal den Wert eins annehmen könnten und die Y-Achse also zwischen null und eins sowie deren Bruchteilen angelegt werden muss. Die X-Achse richtet sich hierbei nach den verschiedenen Klassen.
Hier wähle ich den Maximalwert 0,5 für die Y-Achse, da die "Höhe" den Wert 0,39 nicht übersteigt, und trage für den Wert 0,5 auf dem Papier 10 cm auf der Y-Achse vom Ausgangspunkt als Richtwert ein.
Für die X-Achse wähle ich den Richtwert 15 cm, was im Nachhinein betrachtet ein wenig großzügig bemessen war. Ich zeichne auf der X-Achse alle drei Zentimeter eine Markung für jeweils einen 500er Schritt auf der X-Achse ein. Als Nächstes setze ich den Stift bei dem Wert 750, also der unteren Klassengrenze der untersten Klasse an und zeichne für die "Höhe" 0,39 gemäß der relativen Häufigkeit der Klasse ein. Danach zeichne ich 250 Einheiten auf der X-Achse nach rechts zum X-Wert 1000, was der oberen Klassengrenze der ersten Klasse entspricht und führe anschließend den Stift zum Y-Wert 0 auf der 1000er Markierung hinunter. Die erste Fläche ist geschafft!
Danach zeichne ich von der 1000er Marke nach oben zum Y-Wert 0,29 hinauf und dann wieder nach rechts 250 Einheiten und wieder runter zur 1250er Markierung. So wird von Fläche zu Fläche gesprungen, bis alle Klassen durchgezeichnet sind.
Bei letzten Fläche ist die Höhe halbiert, aber dafür ist die Fläche auch zweimal so breit wie anderen. Die relativen Häufigkeiten geben die Flächen der einzelnen Klassen des Histogramms an und weil die Klassenbreite dieser Klasse doppelt so groß ist muss die "Höhe" halbiert werden. Wäre die Klassenbreite dreimal so groß wie die der anderen müsste sie gedrittelt werden und so weiter und so fort. Vielen Dank für Ihre Aufmerksamkeit.
Histogramm mit Erklärungen
Bildquelle:
johannes flörsch
(So findest du die Sternschnuppen der Perseiden)
Karin Scherbart
(Wie macht man einen Regenbogen selbst?)