Was sind Bäume und Binärbäume in der Informatik

Was sind Bäume in der Informatik?

Um Binärbäume verstehen zu können, muss man erst einmal wissen, was eigentlich ein Baum in der Informatik allgemein ist. Wie so häufig, kann man bei diesem Wort durchaus Parallelen zu dem Wort in der Realität finden: Ein Baum findet seinen Anfang in der Wurzel. Dann folgt ein Stamm, von dem große Äste abzweigen. Von den großen Ästen zweigen kleinere Äste ab und von diesen können noch einmal kleinere Äste abzweigen und so weiter. An den dünnen Zweigen hängen schließlich die Blätter. Nach den Blättern folgen keine weiteren Äste mehr und auch keine weiteren Blätter. Sie sind die Endpunkte.

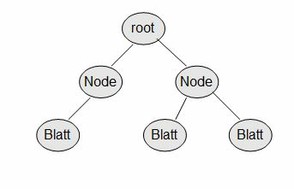
Wenn Sie dieses Prinzip aus der Realität verstanden haben, haben Sie schon fast Informatik-Bäume verstanden. Auch diese beginnen bei einer Wurzel ("root"), die im Gegensatz zu realen Bäumen "oben" steht. Nun zweigen von der Wurzel Äste ab, die in der Informatik als "Kanten" bezeichnet werden (engl. "Edge"). Die Abzweigungen selbst werden "Knoten" genannt (engl. "Node"). Wie bei einem realen Baum können an Kanten Knoten stehen, von denen weitere Kanten abzweigen, die wiederum in Knoten und weitere Abzweigungen weiterlaufen. Das Ende bilden die sog. "Blätter". Diese haben keine Nachfolger mehr. Knoten, die auf derselben "Höhe" stehen, befinden sich auf einer Ebene.

Der Gesamtbaum hat nur eine einzige Wurzel, aber jeder Knoten kann wiederum als Wurzel eines Teilbaums betrachtet werden. Wenn Sie einen beliebigen Teilbaum entnehmen, werden Sie immer eine eindeutige Wurzel haben. Zwischen der Wurzel und jedem Knoten bzw. jedem Blatt kann es immer nur einen einzigen Weg geben. Wie viele Nachfolger ein Knoten haben darf, hängt von der Art des Baums ab.

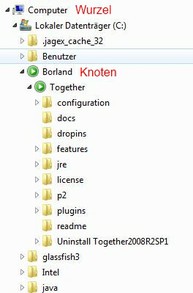
Ein Beispiel für einen solchen Baum ist das Dateisystem von Windows: Der Arbeitsplatz stellt die Wurzel dar. Dort zweigen die Laufwerke ab, dann die Ordner. In den Ordnern können weitere Ordner stecken, in denen sich wieder Ordner befinden können. Die Dateien können keine weiteren Ordner enthalten - sie sind die Blätter des Baums. Jede Datei hat einen sogenannten Pfad - das ist der Weg durch den Baum bis zu dieser Datei. Dieser Pfad ist immer eindeutig.

Was soll das mit diesen Bäumen?

Bäume sind eine äußerst effiziente Datenstruktur, weil die Suche nach Daten sehr schnell abläuft. Denken Sie an den Dateibaum von Windows. Durch den eindeutigen Pfad sind Sie in der Lage, eine bestimmte Datei sehr schnell zu finden. Wenn Sie eine neue Datei erstellen wollen, können Sie (theoretisch - gute Ordnerstruktur vorausgesetzt) sofort den Ort ausfindig machen, wo Sie die Datei erstellen müssen. Sie müssen nicht jede einzelne Datei auf Ihrer Festplatte betrachten, sondern können durch die Baumstruktur sehr schnell an eine bestimmte Stelle navigieren.

Binärbäume im Detail

Nun ist geklärt, um was es sich bei Bäumen handelt. Bei Bäumen gibt es verschiedene Untergruppen. Eine von ihnen ist der sogenannte Binärbaum. Die Besonderheit bei diesem Baum ist, dass jeder Knoten maximal zwei Nachfolger haben darf. Die Daten befinden sich in den Knoten oder in den Blättern und zwar pro Blatt und pro Knoten genau eine Information.

Eine Analogie für das Funktionsprinzip eines Binärbaums kann ein Telefonbuch dienen. Wenn Sie nach einem Namen (z.B. Thomas Wiegand) suchen, schlagen Sie das Telefonbuch in der Mitte auf. Da das Telefonbuch alphabetisch sortiert ist, können Sie mit Sicherheit sagen, dass der gesuchte Name in der hinteren Hälfte stehen muss. Also lassen Sie die erste Hälfte außer acht und schlagen die zweite Hälfte in der Mitte auf. Wieder können Sie sagen, dass der gesuchte Name in der zweiten Hälfte liegen muss. Sie haben also mit zwei Suchoperationen bereits drei Viertel des gesamten Telefonbuchs ausgeschlossen. Sie sehen, dass Sie auf diese Art sehr schnell und effizient nach einem Namen suchen können.

Nun betrachten Sie einmal den Binärbaum im Bild. Der Binärbaum ist folgendermaßen aufgebaut: Links von einem Knoten steht der kleinere Wert, rechts der größere. Nun gehen wir ähnlich vor wie bei dem Telefonbuch, wenn wir die 100 suchen. Wir beginnen bei der Wurzel, der 50. Da 100 größer ist als 50, können wir die gesamte linke Hälfte des Baums ausschließen. Hier kann sich die gesuchte Zahl nicht befinden. Wir betrachten den nächsten Knoten, die 70. Die 100 ist größer als die 70, also müssen wir auch hier den rechten Teilbaum betrachten. Als nächstes finden wir die 200. Unsere gesuchte Zahl ist kleiner: Wir suchen links weiter und finden im nächsten Knoten tatsächlich die gesuchte Zahl.

Aber warum sind die Zahlen so seltsam sortiert? Das hat mit dem Einfügen in einen Binärbaum zu tun.

Daten in einen Binärbaum einfügen

Die Regel beim Einfügen von Daten ist bereits erwähnt worden: Ein kleinerer Wert wird links eingefügt, ein größerer rechts. Dabei werden die Werte entsprechend ihrer Reihenfolge eingefügt und die richtige Einfügestelle muss zuerst gesucht werden, damit die Sortierung erhalten bleibt. Sehen wir uns das folgende Beispiel an. Wir möchten diese Zahlen in einen Binärbaum einfügen: 65, 45, 29, 79, 88, 68, 100.

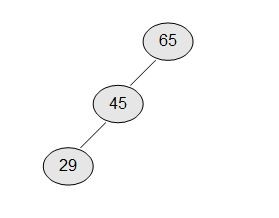
Das erste Element, die 65, ist die Wurzel und steht ganz oben. Betrachten wir die nächste Zahl. Die 45 ist kleiner; sie wird also links an die Wurzel angehängt. Die nächste Zahl, die 29, ist kleiner als die Wurzel. Sie kommt nach links. Leider ist die linke Seite schon belegt. Deswegen betrachten wir die 45, stellen fest, dass die 29 kleiner ist, und fügen sie deswegen links von der 45 ein. Die 79 ist größer als die Wurzel. Folglich kommt sie nach rechts. Und der rechte Platz unterhalb der Wurzel ist noch frei. Also wird die 79 dort eingefügt.

Die 88 ist größer als die Wurzel. Wir marschieren nach rechts. Sie ist aber auch größer als die 79. Sie wird rechts unter die 79 gehängt. Die 68 ist größer als die Wurzel. Wir wandern nach rechts. Aber sie ist kleiner als die 79. Sie kommt an die linke Stelle unter der 79. Und schließlich fügen wir die 100 ein. Sie ist größer als die Wurzel, größer als die 79 und größer als die 88. Wir gehen also drei Mal nach rechts und hängen dort die 100 ein.

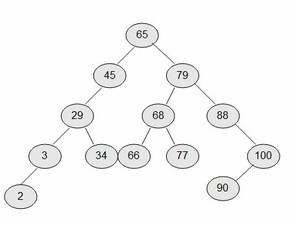
Erweitern Sie den Baum als Übung um die folgenden Zahlen: 3, 77, 6, 66, 34, 90. Die Lösung sehen Sie ganz unten.

Balancierte und unbalancierte Bäume

Erstellen Sie einen Binärbaum aus der folgenden Liste: 1, 5, 6, 14, 15, 20, 24. Sie werden ganz schnell ein Problem feststellen: Die kleineste Zahl, die 1, ist die Wurzel. Alle anderen Zahlen sind größer, sie werden also immer rechts eingefügt. Weil die Liste sortiert ist, "hängt" unser Baum in eine Richtung: Der rechte Ast ist viel zu "schwer". Das bekommt einem natürlichen Baum nicht gut und unserem künstlichen auch nicht. Wir haben nichts gewonnen: Unser Baum ist weiterhin eine Liste; er ist "unbalanciert".

Ein Baum wird balanciert genannt, wenn die Daten auf allen Seiten aller Teilbäume ungefähr gleich verteilt sind. Im nächsten Bild sehen Sie einen balancierten Baum. Bäume sollten so gut balanciert sein wie möglich, denn bei einem unbalancierten Baum werden die Pfade länger und damit dauern sämtliche Operationen länger.

Ausblick

Das Thema des nächsten Artikels sind gängige Operationen in Binärbäumen wie Löschen von Daten. Des Weiteren sollen Varianten von Bäumen vorgestellt werden, die sich selbst balancieren, was der Binärbaum nicht schafft, z.B. Rot-Schwarz-Baum oder der 2-3-4-Baum.